中图分类号：TU 443                     文献标识码：A

Study on The Influence of Shear Deformation on The Internal Stress of Plate Rubber Bearing Based on Different Shapes

Bi Jian

( Gezhouba Wuhan road Materials Co., Ltd., Hubei, Wuhan 430000, China )

Abstract: In order to explore the internal stress distribution of circular plate rubber bearing and rectangular plate rubber bearing under different shear deformation conditions, the tangent value of shear Angle tana is proposed to be four different shear Angle values of 0.5, 1.0, 1.5 and 2.0, respectively.  Under the same vertical load, the stress distribution of the steel plate between the internal layers of the bearing after shear deformation is investigated.  The results show that the maximum normal equivalent stress of the middle layer steel plate increases significantly with the increase of the shear Angle of the rubber plate in the round plate rubber bearing, and the stress of the fourth layer steel plate increases the most, when the shear Angle tangent value is 2.0, the increase rate is 87.2%, and the increase rate is 57.9% under the same conditions.  The stress level of the rectangular plate bearing is lower than that of the circular plate bearing under the same shear Angle.  When the shear Angle tana=1.0, the peak value of the two kinds of stiffening plates appears at 140mm away from the center point of the ④ layer stiffening plate.  Compared with the circular plate, the peak normal form equivalent stress of the rectangular plate is reduced by 9.7%.  With the increase of shear Angle, the maximum principal tensile stress of rubber between the stiffened plates almost presents a linear increase trend, and the difference value of the maximum principal tensile stress of rubber between the circular plate and the rectangular plate almost remains unchanged at about 8MPa at each shear Angle.

Key words: plate rubber bearing; shear deformation; stress distribution; form factor

公路桥梁板式橡胶支座剪切变形病害在现状桥梁结构中最为常见，支座剪切变形产生的原因较多，常见的因素在于汽车或地震等动荷载作用下引起的支座变形，对于板式橡胶支座而言，因其结构简单，生产便利，造价成本较低，安装便捷等优点，被广泛应用于梁式桥中，因为现存板式橡胶支座数量庞大，加之其结构简单，绝大部分使用中的板式橡胶支座均存在不同程度的剪切变形，严重着甚至发生破裂变形，影响桥梁结构安全性能^[1]。工程中常见的板式橡胶支座按形状分为圆形和矩形，对于板式橡胶支座剪切变形的研究目前已较为深入，项乃亮、崔侠侠等以地震中的支座滑移典型病害工程实例为背景，对支座的滑动摩擦性能进行了研究^[2]；董振华、贺存哲等研究了考虑摩擦滑移条件下的板式橡胶支座剪切性能，试验表明摩擦条件对支座水平侧移和抗侧力的影响较大^[3]；孙新阳，杨维国等通过数值模拟和理论分析，推导了不同界面形状下板式橡胶支座剪切变形条件下的压缩刚度比公式，并通过试验证明了该组公式的合理性^[4]；金建敏、肖骥等对橡胶隔震支座开展了压缩性能试验，推导了不同剪切变形下橡胶隔震支座竖向压缩刚度计算方法，并验证了橡胶隔震支座竖向压缩刚度与剪切应变程正相关^[5]。

结合上述分析，对于板式橡胶支座剪切变形对支座承载性能的理论研究已经相对比较深入，随着工程技术的推进，新式支座在桥梁工程中的应用也越来越广泛，但对于现存服役的板式橡胶支座，剪切变形带来的桥梁结构安全隐患任然存在，在此基础上，为探究圆形板式橡胶支座与矩形板式橡胶支座在不同剪切变形条件下，支座内部应力分布情况，特通过数值模拟的方式，分析不同剪切角度下的支座内力分布情况。

1  数值模拟

1.1   数值模拟参数设置

为探究圆形板式橡胶支座与矩形板式橡胶支座在不同剪切角度条件下的钢板内力与橡胶应力状态，选取工程中较为常用的两种支座进行数值模拟研究，两种支座总厚度均为74mm，单层橡胶厚度8mm，共六层，单层钢板厚度为3mm，共七层，上下顶面橡胶保护层厚度为2.5mm，其他尺寸及工程力学参数如表1所示：

表1  预应力损失系数表k

根据橡胶与钢板两种材料的力学性质及性能表现，假定数值模拟过程中的橡胶材料与加劲薄钢板均处于弹性变形状态（忽略橡胶材料初始非线性变形），且数值模拟过程中，支座不发生材料破坏。

以MIDAS civil为数值模拟工具建立数值模拟模型如图1所示，选用四边形网格划分模型，网格密度为5mm×5mm×5mm，根据工程实际情况，拟定支座竖向荷载为10MPa，通过改变支座横向荷载控制其剪切变形量，控制变量剪切角度正切值tana分别为0.5、1.0、1.5、2.0。

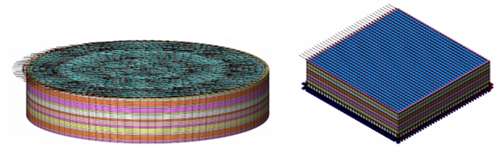
图1 数值模拟分析模型

1.2   不同剪切变形加劲板最大应力分布

由于板式橡胶支座在横向荷载作用过程中，加劲板应力分布并不均衡，为描述加劲板材料强度及韧性等力学性质，采用等效单轴应力对其进行描述，该等效应力成为范式等效应力（Von mises），以下研究结果中提到的加劲板应力均为范式等效应力，提取两种不同形状的板式橡胶支座各加劲板最大等效应力结果，绘制应力曲线如图2图3所示。

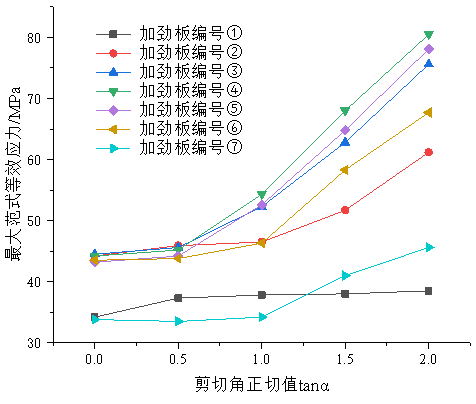
图2 圆形板式橡胶支座加劲板应力分布曲线

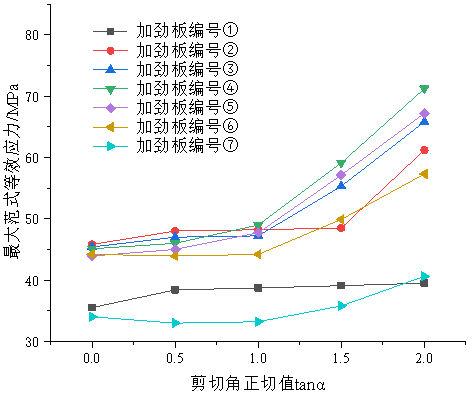
图3 矩形板式橡胶支座加劲板应力分布曲线

图2图3分别描述了不同剪切变形条件下，板式橡胶支座最大范式等效应力值变化情况，支座中加劲板自上而下依次编号，最上层为①，最下层为⑦，整体趋势来看，随剪切角正切值tana分别为由0增大至2.0过程中，各层加劲板应力均呈现增长趋势，顶层和底层加劲板应力整体变化幅度不大，且应力水平均处于较低状态，位于中间层的④号加劲板应力变化幅度最大，在圆形板式橡胶支座中，tana为0时（支座仅受轴向压力），最大应力值为44.2MPa，tana=1时，最大应力值为54.3MPa，增加了22.9%，当tana=2.0时，最大应力值增大至80.5MPa，增长幅度为82.2%；在矩形板式橡胶支座中，tana为0时（支座仅受轴向压力），最大应力值为45.1MPa，tana=1时，最大应力值为49MPa，增加了8.6%，当tana=2.0时，最大应力值增大至71.2MPa，增长幅度为57.9%。

对比两种不同形状的板式橡胶支座在相同剪切角度条件下加劲板应力可以看出，矩形板式橡胶支座加劲板最大范式等效应力均小于圆形板式支座，且矩形板在剪切角度tana≤1时，各层间加劲板应力变化幅度均低于10%，而圆形板在tana≤0.5时才有此表现，超过0.5后，应力即会出现陡增的现象。

1.3   剪切角tana=1.0时加劲板应力平面分布

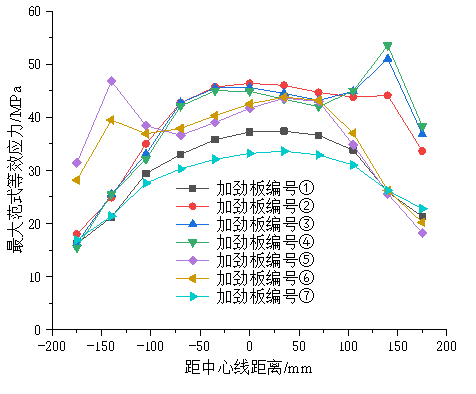
图4 剪切角tana=1.0时圆形板应力水平分布曲线

图4 剪切角tana=1.0时矩形板应力水平分布曲线

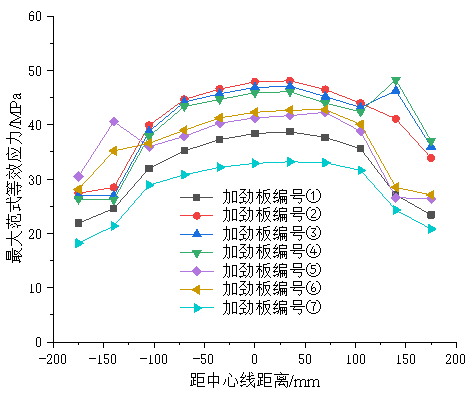
在桥梁检测及加固实际工程中，根据《公路桥梁板式橡胶支座》规定，支座剪切角度不应超过35°，超过该限度时，需对支座进行处理，此时剪切角正切值tana=0.7，为探究工程中剪切值超限的板式橡胶支座加劲板应力表现情况，特拟定剪切角度为tana=1＞0.7时的圆形和矩形橡胶支座为研究对象，此时剪切角度为45°＞35°，以圆心（矩形板中以中心点）为坐标原点，间隔35mm，提取两种支座各层间加劲板横轴方向最大范式等效应力，由此得到tana=1.0时板式橡胶支座应力水平分布曲线如图4图5所示。

分析图中曲线可以看出，顶层及底层加劲板应力呈现先增大后减小的趋势，其沿横轴方向呈现出规律性变化趋势，且应力峰值在两种形状的支座中均为最低值，其余各层加劲板应力峰值均不在中心点出，第⑤层和第⑥层加劲板应力峰值出现在距中心点-140mm处，第②③④层加劲板应力峰值出现在距中心点140mm处，所有加劲板应力峰值任然为第④加劲板。

对比不同形状板式橡胶支座应力水平分布曲线，在矩形橡胶板中，各层加劲板应力变化在中心点附近的变化更为均衡，表现为距中心线-105mm~105mm之间，矩形边应力曲线接近与水平状态，而在圆形板中，各层加劲板应力曲线不均衡；两种支座加劲板峰值均出现在第④层加劲板距中心点140mm处，其中圆形板峰值范式等效应力为53.5MPa，矩形板最大值为48.3MPa，相较于圆形板降低了9.7%。

1.4   不同剪切变形橡胶最大主拉应力分布

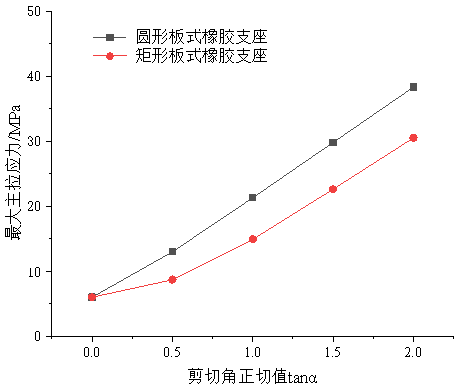
图5 剪切角度对橡胶最大主拉应力影响曲线

如图5所示为不同剪切变形条件下，加劲板层间橡胶的最大主拉应力变化情况，从板式橡胶支座结构组成可以看出，加劲板层间的天然橡胶是板式橡胶支座能够产生变形的结构所在，天然橡胶具有良好的变形能力，在剪切角度不大的情况下，橡胶能够随荷载作用发生不同程度的变形，工程中认为，支座剪切角度不超过35°时，支座内的橡胶结构处于弹性变形阶段，橡胶与加劲板之间通过化学粘结作用形成一个整体，在竖向荷载作用，钢板能够有效限制橡胶的侧向位移，承担竖向荷载，而橡胶亦能在钢板之间传递荷载，评价橡胶力学性能的指标为最大主拉应力。

结合图5分析可知，随剪切角度增大，加劲板间橡胶的最大主拉应力几乎呈现线性增长趋势，但圆形板与矩形板最大主拉应力在相同剪切角度下存在差异，当tana=1时，圆形板橡胶最大主拉应力为21.6MPa，矩形板橡胶最大主拉应力为13.4MPa，相差8.2MPa，且各剪切角度下，圆形板与矩形板橡胶最大主拉应力相差值几乎保持不变在8MPa左右，反映到剪切角度对橡胶最大主拉应力影响曲线中表现为两条曲线几乎保持平衡。

2  形状因素对支座内力影响分析

根据数值模拟结果及板式橡胶支座内力分析结果可以看出，两种不同形状的板式橡胶支座在不同剪切值下的应力表现存在差异，数值模拟过程中，对两种支座的力学参数取值均保持一致，仅在形状上存在差异，由此可以看出，形状因素对支座内力存在较大影响。

2.1形状系数

支座形状系数是反映支座受压过程中，受压面积与自由膨胀面积的比值，其值大小能够反映支座竖向变形的能力，根据形状系数的定义，两种形状的支座形状系数S计算公式为：

        （1）

其中，l₀、l₁分别为矩支座加劲板边长，mm，D₀为圆形板承载截面的水平投影直径，mm；h为中间层单层橡胶层厚度，mm。根据1.1节中数值模拟参数计算得到，矩形与圆形板式支座的截面形状系数均为10.63，表明两种形状的板式橡胶支座在抵抗竖向变形方面能力表现一致。

2.2水平位移

在板式橡胶支座的双弹簧模型中，橡胶支座在承受剪切变形后，其力学模型仅与剪切刚度和转动刚度两个因素有关，在横向荷载作用下，板式橡胶支座顶端水平位u移计算公式为：

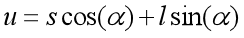        （2）

其中s为模型水平弹簧变位，l为刚性柱长，为剪切角度，两种形状的板式橡胶支座，其刚性柱长l在支座厚度选择过程中就已经确定，此参数仅与支座中加劲板与橡胶厚度有关，而水平弹簧变位s却与形状存在较大关系，在圆形板中，s运动方向可视为π/2，在水平荷载和竖向荷载共同作用下，圆形板式支座水平弹簧变位为空间合成位移，而在矩形板中，水平弹簧仅能沿作用力反向移动，为平面水平变位^[6][7]。因此导致相同水平荷载作用条件下，圆形橡胶板水平变位大于矩形板，数值模拟过程中假定剪切角度α相同，此时圆形板顶面水平位移将大于矩形板，结合数值模拟结果可知，此时支座内部的加劲板与橡胶板变位在圆形板中更大，这也解释了数值模拟过程中圆形支座加劲板范式等效应力更大的原因。

2.3有效面积

剪切变形后支座的有效面积为支座上顶面与下地面重合的面积，在有效面积模型中，支座剪切变形后，真正承担竖向工作荷载的范围不包含变形后上顶面及下底面错位的面积^[8]。根据此理论条件，在相同剪切变形作用下，矩形板式橡胶支座有效面积A_eq为：

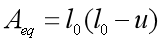        （3）

矩形板式橡胶支座有效面积A_ep为:

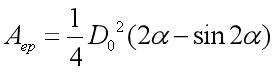        （4）

对比不难看出，当形状参数一致时，，表明在相同剪切角度下，矩形板有效面积较大，这也解释了在相同竖向荷载作用下，加劲板间橡胶最大主拉应力的数值模拟结果。

3  工程应用

图6 某大桥支座剪切变形超限

如图6所示为贵州某大桥支座剪切变形现场照片，图中可以判断该支座存在剪切变形超限、支座脱空等病害，需对其进行更换处理，经过现场数据测算，板式橡胶支座承受的最大反力为R_ck=792kN，桥梁转动角横桥向和纵桥向分别为1.08×10^-3rand和3.94×10^-3rand，拟选用数值模拟中相同尺寸的350×350×74mm的矩形板式橡胶支座对其进行更换处理。

选用支座总厚74mm，单层橡胶层厚度为8mm，共6层；保护层橡胶厚2.5mm，2层；中间钢板3mm，共7层，加劲钢板边长l₀橡胶层总厚t_e=6×8+2×2.5=53mm。

支座平均应力：

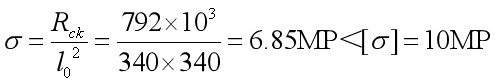
平均应力满足规范要求

转角验算：

支座压缩变形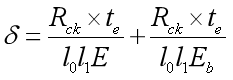

其中抗压弹性模量E=5.4GS²，剪切模量G=1MPa，形状系数S=10.63，带入以上数据可得E=610MPa，加劲钢板E_b=2000MPa，带入上述数据可得支座压缩变形为0.78mm。

当转角为3.94×10^-3rand时，由转动引起的剪切变形，表明支座在转动条件下的竖向压缩变形大于剪切变形，支座不会发生脱空。

支座抗滑移验算：

支座产生的摩阻力为μR_ck=0.3×792=100.26kN,根据结构验算结果，单个支座所承受的结构制动力为42.35kN，小于支座摩阻力，表明支座不会发生滑动。

综上所述，选用350×350×74mm的矩形板式橡胶支座对旧支座进行更换，其结构受力均能满足设计要求。

4  结论

通过对不同形状板式橡胶支座的数值模拟分析，探究了圆形板式橡胶支座与矩形板式橡胶支座在不同剪切变形条件下，支座内部应力分布情况，得到以下主要结论：

（1）在圆形板式橡胶支座中，随橡胶板剪切角度增加，中间层钢板最大范式等效应力大幅度增加，其中第4层钢板应力增幅最大，剪切角度正切值为2.0时，增加幅度达87.2%，相同条件下，矩形支座增幅为57.9%。

（2）矩形板式支座应力水平均低于同剪切角度条件下的圆形板式支座应力，当剪切角tana=1.0时，两种支座加劲板峰值均出现在第④层加劲板距中心点140mm处，矩形板相较于圆形板，峰值范式等效应力降低了9.7%。

（3）随剪切角度增大，加劲板间橡胶的最大主拉应力几乎呈现线性增长趋势，各剪切角度下，圆形板与矩形板橡胶最大主拉应力相差值几乎保持不变在8MPa左右。

参  考  文  献

[1] 许汉铮,刘注,展艳凯等.板式橡胶支座的水平位移特性[J].科学技术与工程,2023,23(07):3038-3044.

[2] 金建敏,肖骥,刘彦辉等.不同剪切变形下橡胶隔震支座竖向压缩刚度试验研究[J].振动与冲击,2021,40(06):93-99.

[3] 邱文,邹开泰.高速公路桥梁支座病害分析及修复[J].公路,2021,66(02):129-132.

[4] [4]董振华,贺存哲,程寿山等.考虑摩擦滑移的普通板式橡胶支座剪切性能研究[J].中国公路学报,2020,33(02):83-93.

[5] 孙新阳,杨维国,王萌等.剪切变形下橡胶支座压缩刚度比分析研究[J].工程力学,2017,34(01):58-68.

[6] 李冲,王克海,李悦等.板式橡胶支座摩擦滑移抗震性能试验研究[J].东南大学学报(自然科学版),2014,44(01):162-167.

[7] 李枝军,葛飞,徐秀丽等.板式橡胶支座性能有限元模拟与试验研究[J].东南大学学报(自然科学版),2013,43(06):1299-1304.

[8] 韩强,刘文光,杜修力等.桥梁隔震支座压缩剪切变形状态的竖向刚度研究[J].世界桥梁,2006(01):52-55.